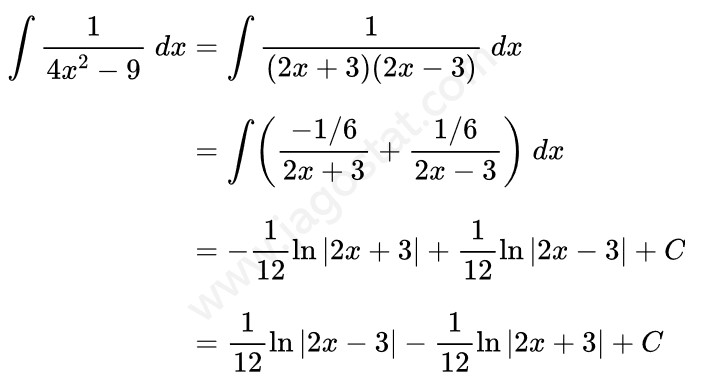Bahas Soal Matematika   »     ›  

Tentukan hasil dari \( \int \frac{1}{4x^2-9} \ dx = \cdots \ ? \)

Pembahasan:

Fungsi penyebut pada integran mengandung faktor linear yang berlainan sehingga bentuk integralnya bisa diubah menjadi:

Selanjutnya adalah mencari nilai \(A\) dan \(B\). Perhatikan berikut ini:

Dari persamaan di atas, diperoleh hubungan antara A dan B sebagai berikut:

Dengan menyelesaikan hasil di atas, diperoleh nilai \(A = -\frac{1}{6} \) dan \(B=\frac{1}{6} \). Dengan demikian,